
Experiments
DEREK is a simple yet powerful environment for the study of dynamical systems. The program includes a variety of well-known dynamical systems with which you can experiment. Next, we consider several such experiments.
Controlling the satellite
Following the description in the book: E. Hairer, S.P.Nørsett, G. Wanner, Solving ordinary differential equations: Nonstiff problems (publishing Springer Science & Business Media, 1993, p.129), we consider the classical problem of three bodies with mass and obeying the law of gravity . Assume that the mass of the third body is negligibly small compared with the first two masses, and - that the three bodies move in one plane - an example of such system may be an artificial satellite motion in the gravitational field of the Earth and the Moon. The system of equations of motion in this case is following:
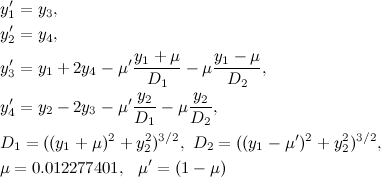
Periodic orbits attract a special interest among all possible movements in this system. Careful choice of the initial conditions:
mentioned in the book, allows you by solving the system to get an interesting periodic orbit (similar orbits are called «Arenstorf orbits»)
In the DEREK database there is a description of the system (file) ARENST, in which the equalions of three-body problem are presented in the following form:
The solution of this system using DEREK allows to see the orbit mentioned above - satellite writes out intricate (and repetitive) «pretzels» around the Earth and the Moon:

Now we can set the following problem - how to return to the Earth (to land) the satellite orbiting Arenstorf orbit? Assume that the satellite has its own engine, which at a certain point we can turn on that will give some constant acceleration to the satellite, and then turn it off after a little time gone. In this case, the equations of motion take the form:
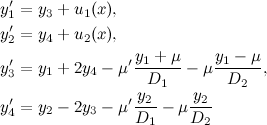
where
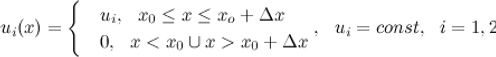
Let's try to examine this problem by using DEREK. For our experiment, copy the description of the system for the Arenstorf orbit ARENST from DEREK database and save it as a new description named SATCTRL, trying to take into account the operation on and off of the engine in the equations:
-
C3 denotes the time at which the engine starts
-
C4 - the time interval during which the engine is running,
-
C5 and C6 - values of respectively horizontal and vertical component of a constant acceleration imparted to the satellite.
We will explore the new system (run the animation)
In the same way, you can try to land a satellite on the Moon by selecting the appropriate time to enable the engine, its duration and thrust.
By the way, the orbits of such type have been used in real flights to the Moon, which were carried out within the framework of the «Apollo» US lunar program . On the next frame from the American «Apollo 13» movie there is a screen in the Mission Control Center showing an Arenstorf orbit as «eight», with the Earth and the Moon in its different rings.
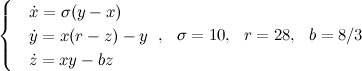
The paper Vadim G. Prokopenko, «Reduplication of chaotic attractors and construction of compound multiattractors»,Nelin. Dinam., 8:3 (2012), 483–496 (in russian) , proposed an interesting modification of this system that can be reproduced using DEREK.
Thus, the description of the Lorenz system in a DEREK database called LORENZ and has the following form:
In the above paper, the author proposes to replace one of the variables that denote the components of the dynamical system (e.g., X) with piecewise linear function of special form:
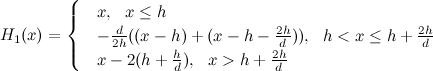
The graph of this function is shown below:
The equations of the new system will be:

In the modified system occurs the «reproduction» of the Lorenz attractor, when two attractors arise instead of single «butterfly» attractor. DEREK can easily demonstrate it. Copy the description of the classical Lorenz system LORENZ, making appropriate changes to the equations and save the new description under the name REDUPL:
In this description, C4 denotes h, a C5 - d, the specific values of used here h and d, proposed by the author, are:
h = 18, d = 10
Now we can watch for the reduplication of the attractor (start the animation):
In mentioned work, the author offers a further extension of this design, which allows you to get an attractor consisting of a set of elementary attractors, but this is beyond the scope of this experiment. The details can be found in the full text of the article: http://nd.ics.org.ru/doc/r/pdf/2049/1 (in russuan).
It's hard to resist to say something like: «The author has demonstrated a new way of butterflies breeding» ☻!

As you can see, by using DEREK it's quite simple to implement fairly complex experiments with the real dynamical systems.

