Показатели Ляпунова

Что такое показатель Ляпунова

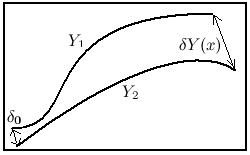
Показатели Ляпунова динамической системы с непрерывным временем определяют степень расхождения (или сближения) различных, но близких траекторий динамической системы на бесконечности. Если в начальный момент две различные траектории находятся на расстоянии δ0 друг от друга, то по прошествии достаточно большого времени x расстояние между ними будет выглядеть как:

где λ - показатель Ляпунова. Для различных начальных условий числа λ могут быть разными. Если соответствующий показатель Ляпунова положителен, расстояние между изначально близкими траекториями системы увеличивается со временем, если показатель отрицательный - близкие траектории становятся еще ближе, наконец, если показатель равен нулю - близкие траектории остаются примерно на том же расстоянии друг от друга. Известно, что для N-мерной динамической системы существует ровно N показателей Ляпунова λ1 ≥ λ2 ≥ ...≥ λN, в общем случае, различных (теорема Оселедца (англ.), это верно для «почти всех» начальных состояний динамической системы). Набор показателей Ляпунова (спектр) характеризует общие закономерности поведения системы для всех возможных начальных условий.

Показатели Ляпунова произвольной динамической системы редко могут быть получены аналитически (в виде формулы), но существуют численные методы, позволяющие их вычислить с приемлемой точностью.

Показатели Ляпунова важны в качественной теории динамических систем. Знание показателей Ляпунова позволяет сделать вывод об общем поведении системы с течением времени. Часто достаточно знать ЗНАК первого, т.е. максимального показателя и ОБЩУЮ СУММУ показателей.

В трехмерном случае для систем вида:

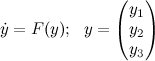
если рассматривать только системы, имеющие физический смысл, для которых не все показатели Ляпунова положительны и их сумма не положительна, и обозначить знаком «-» отрицательный показатель Ляпунова, знаком «+» положительный, а знаком «0» - нулевой, тогда доступны следующие различные варианты поведения:

(-,-,-) система стремится к фиксированной точке, т.е. к стационарному состоянию, не зависящему от времени
(0,-,-) поведение системы становится периодическим, ее траектория приближается к замкнутой кривой (такая кривая называется «предельным циклом»)
(0,0,-) квазипериодическое поведение, при этом траектории системы находятся на поверхности двумерного тора, т.е. «бублика»
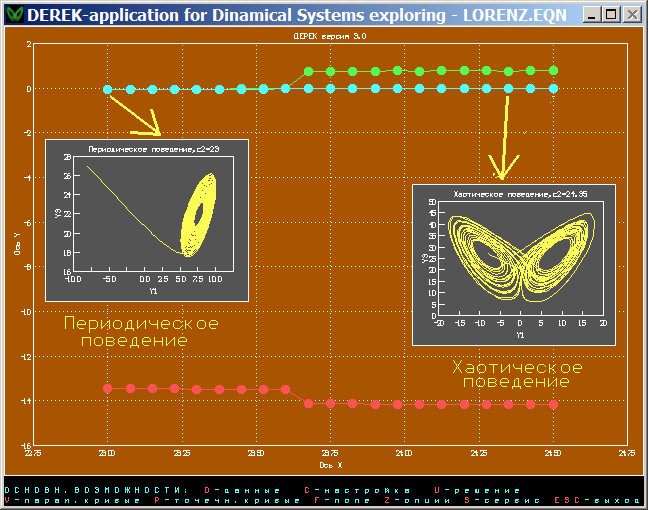
(+,0,-) с течением времени система приближается к «странному аттрактору» (примером может служить система Лоренца), поведение системы можно назвать хаотическим.

Для систем более высокой размерности набор вариантов становится более обширным, однако по-прежнему наличие положительного показателя Ляпунова (при условии отрицательности их суммы) влечет за собой хаотическое поведение

Численное определение показателей Ляпунова

DEREK умеет вычислять часть спектра показателей Ляпунова (не более 4-х первых показателей, если расположить их в порядке убывания, т.е. для систем не более четвертого порядка определяются ВСЕ показатели ), пользуясь численным итерационным алгоритмом Бенеттина (англ.). Согласно этому алгоритму показатели Ляпунова можно найти с помощью многократного решения вспомогательной динамической системы, которая строится на основании исходной. Для реализации этого алгоритма должны быть заданы начальный шаг по времени (по x), точность решения системы, максимальное количество итераций и точность, с которой будут вычислены показатели Ляпунова. Если заранее известно, что у системы есть нулевой показатель Ляпунова (это справедливо, например, для автономной системы, траектория которой не приближается к неподвижной точке) - можно указать соответствующий признак, это повысит точность расчета.

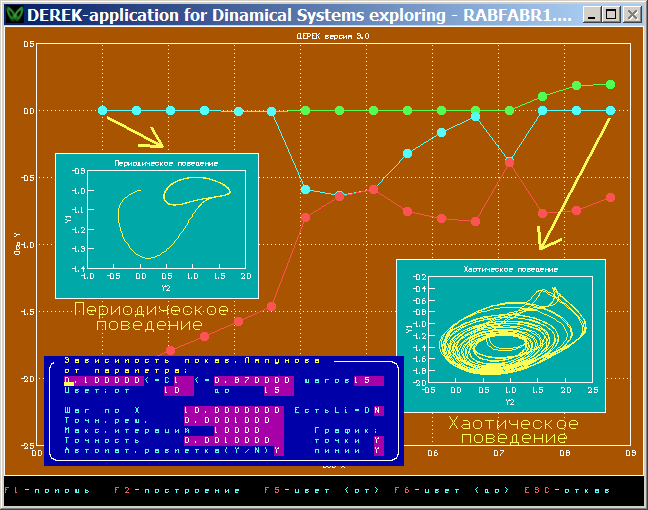
DEREK позволяет также построить график зависимости нескольких старших показателей Ляпунова от параметра системы. Для построения необходимо задать диапазон изменения параметра и количество шагов, на которые этот диапазон будет разбит. В результате работы будет выведен набор графиков, показывающих зависимость каждого из показателей от параметра (в точках, соответствующих шагам). График может быть составлен из отдельных точек (крупных), соединительных линий или и того, и другого.

Для вычисления показателей Ляпунова с помощью DEREKа не требуется никакого дополнительного программного обеспечения - ни компиляторов, ни библиотек программ, ни пакетов компьютерной алгебры. Кроме того, от пользователя не требуется никаких навыков программирования. Все очень просто - необходимо записать уравнения, определяющие динамическую систему, затем выбрать в меню графического окна системы пункт для вычисления показателей Ляпунова, задать несколько (немного) установочных параметров (или воспользоваться установками по умолчанию). После этого можно вычислить численные значения показателей Ляпунова или построить графики зависимости показателей от параметра (константы) системы.

Примеры вычисления показателей Ляпунова

Ниже представлены зависимости показателей Ляпунова от параметра системы для некоторых известных динамических систем.

Система Рабиновича-Фабриканта

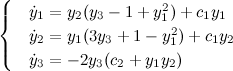
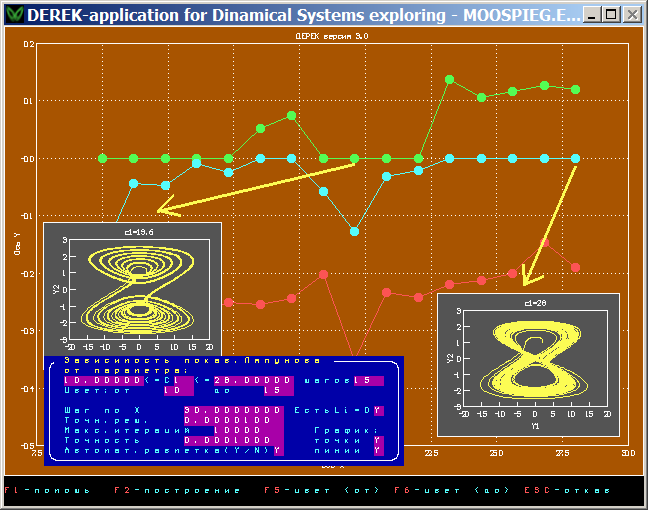
Модель Мура-Шпигеля

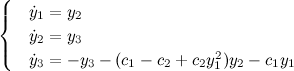
Модель Лоренца

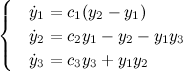
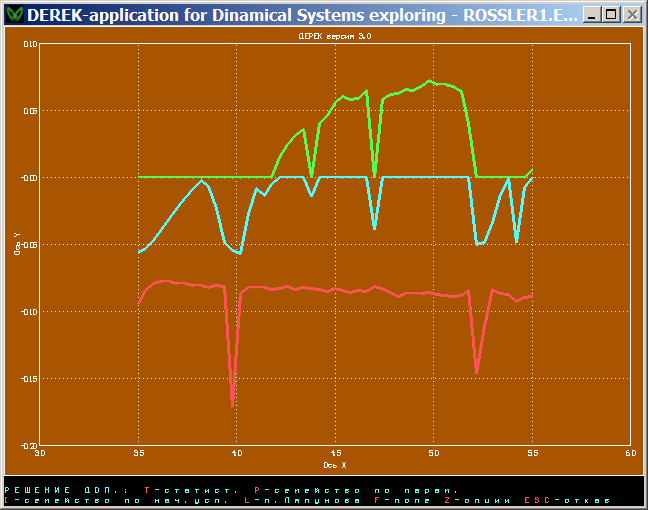
Модель Рёсслера

При изменении параметра c3 в точке c3 ≈ 4.2 поведение системы изменяется с периодического на хаотическое, при дальнейшем увеличении параметра поведение при некоторых значениях возвращается к периодическому.

Генератор квазипериодических колебаний

(См. статью В.С.Анищенко и С.М.Николаева «Генератор квазипериодических колебаний. Бифуркация удвоения двумерного тора»)

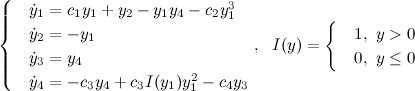
При минимальном значении параметра поведение системы можно квалифицировать как «квазипериодическое» (на это указывают точки сечения Пуанкаре, располагающиеся на двух замкнутых кривых), при максимальном значении параметра система ведет себя хаотически (точки сечения Пуанкаре плотно заполняют некоторую область).

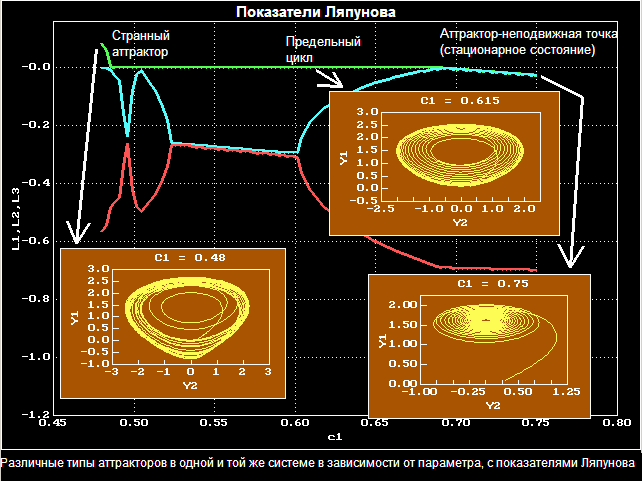
Квазиобратимая система

В статье «Shilnikov bifurcation: stationary quasi-reversal bifurcation» by Marcel G. Clerc, Pablo C. Encina and Enriquie Tirapegui изучается следующая система:

При изменении c1 в заданном диапазоне система демонстрирует различные типы аттракторов. Если c1 меньше, чем 0.48, аттрактор системы - это фиксированная точка, но не конечная (решение стремится к бесконечности).

Более подробную информацию об исследовании динамических систем с помощью показателей Ляпунова можно почерпнуть в курсе лекций С.П.Кузнецова «Динамический хаос»

Памятник А.М.Ляпунову, расположенный возле одного из корпусов ХНУ им. В.Н.Каразина