«Полезно решать дифференциальные уравнения» (сэр Исаак Ньютон)

Реконструкция динамических систем
С помощью динамических систем можно описывать самые разнообразные явления, происходящие в природе и человеческом обществе. Во многих случаях дифференциальные уравнения, описывающие динамическую систему, можно вывести из некоторых законов природы, открытых экспериментально и подтвержденных последующими многочисленными наблюдениями и экспериментами (пример - закон всемирного тяготения, который позволяет выписать уравнения движения планет Солнечной системы и искусственных спутников, находящихся в поле тяготения планет и Солнца). Другой пример такого подхода - это вывод уравнений модели Лоренца на основании системы уравнений гидродинамики - уравнений Навье-Стокса, а также уравнения теплопроводности и уравнения неразрывности (здесь можно познакомиться с подробным выводом).
Однако при исследовании реально существующих систем часто встречается ситуация, когда законы, которым подчиняется функционирование системы, неизвестны. Наблюдая за такой системой, можно лишь измерить один или несколько параметров, ее характеризующих (например, давление или температуру), можно также построить зависимость этих параметров от времени (такая зависимость называется временным рядом). Для подобных систем естественно поставить задачу РЕКОНСТРУКЦИИ, т.е. составления системы дифференциальных уравнений, решением которой является заданный временной ряд (или он в каком-то смысле близок к решению) - если это, конечно, возможно.

В простейшем случае система может быть восстановлена по набору временных рядов (иначе называемому векторным временным рядом), при этом каждый из рядов представляет собой зависимость одной из динамических переменных от времени (т.е. количество рядов совпадает с количеством переменных и равно размерности реконструируемой системы). Система отыскивается в виде:

где y1..yn - динамические переменные, а c1 ..cm - параметры. Значения y1'..yn' находятся при помощи численного дифференцирования соответствующих временных рядов, а в качестве f j(y1..yn,c1..cm) можно взять любые функции, которые удобно использовать для аппроксимации, например, полиномы. Параметры c1 ..cm подбираются так, чтобы решение системы ОДУ было максимально близко к заданному набору временных рядов.
В более сложном случае реконструкция производится только по одному временному ряду (в этом случае он называется скалярным). При этом сначала необходимо проделать реконструкцию динамического пространства, т.е. определить количество динамических переменных (размерность пространства), которые адекватно описывают систему. Размерность может быть известной заранее, а может быть определена с помощью графического анализа данных временного ряда. После определения размерности можно искать реконструируемую систему в виде:

Последовательные производные находятся с помощью последовательного численного дифференцирования исходного временного ряда, а параметры c1..cm функции f(y1..yn,c1..cm) подбираются так, чтобы значения y1(xi) были максимально близки к значениям исходного временного ряда.
Реконструкция систем в DEREKе
DEREK умеет реконструировать систему как для случая векторного, так и скалярного временного ряда. Для тестирования различных методов реконструкции можно использовать модельные динамические системы, получая с помощью DEREKа их решение в виде временного ряда (сохраняемого как простой текстовый файл), а затем применить к такому ряду различные методы и параметры реконструкции и сравнить решения реконструированной системы с решением исходной для определения степени их близости.
Реконструкция по векторному временному ряду на примере системы Лоренца
Рассмотрим реконструкцию для системы Лоренца:

Для реконструкции по векторному временному ряду прежде всего нужно задать (прочитать из файла) описание этого ряда, которое легко получить с помощью DEREK, решив уравнения системы Лоренца:

При реконструкции по векторному временному ряду в DEREK выражения для f j(y1..yn,c1..cm) могут быть заданы в максимально общем виде, лишь бы они зависели линейно от параметров (DEREK сам проверяет линейность). В качестве аппроксимирующего выражения для fj(y1..yn,c1..cm) можно использовать полиномы от переменных y1..yn, линейно зависящие от параметров c1..cm, например:
или любая линейная комбинация базисных функций. Кроме того, выражения для f j могут быть выбраны из множества предопределенных стандартных выражений. Для векторного временного ряда, построенного при решении системы Лоренца, выберем аппроксимирующие функции в виде полиномов второго порядка от переменных y1..yn:

Проделываем реконструкцию и сравниваем результат с исходной кривой:

Реконструкция по скалярному временному ряду на примере системы Рёсслера
Попробуем теперь реконструировать систему по одному скалярному временному ряду, представляющему собой ВТОРУЮ компоненту y2 решения системы Рёсслера:


Для скалярного временного ряда DEREK позволяет сначала произвести оценку размерности реконструируемого пространства. Определение размерности основано на применении теоремы Такенса (англ.),которая утверждает (упрощенно), что, если у динамической системы имеется притягивающее множество (аттрактор), то его изображение можно получить графически, построив зависимость значения временнОго ряда Y(x) в момент времени x от значения того же ряда в момент, взятый с некоторой задержкой: Y(x-τ). Если задержка будет слишком мала, изображение аттрактора будет слишком вытянуто и похоже на отрезок прямой, если слишком велика-изображение не будет иметь ярко выраженную структуру. DEREK позволяет подобрать значение задержки, анализируя зависимость Y(x) от Y(x-τ) для разных τ. На рисунке показан вид восстановленного аттрактора системы Рёсслера для различных значений τ (выраженных в количестве шагов изменения аргумента временного ряда):

Правильно подобранное значение задержки позволяет далее оценить размерность реконструируемой системы по методу Грассбергера-Прокаччиа. Метод Грассбергера-Прокаччиа предполагает анализ графиков зависимости корреляционного интеграла

где
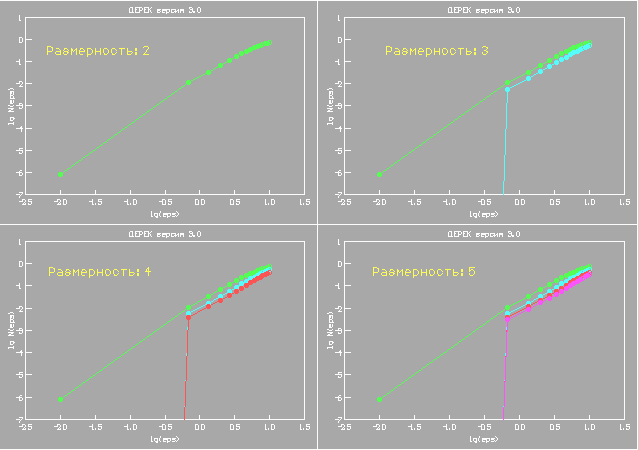
(║.║ - норма вектора, τ - задержка, m - размерность пространства), который представляет собой долю пар точек реконструируемого пространства динамической системы, принадлежащих исходному временному ряду, для которых расстояние между точками пары не превышает ε. Нужно построить графики зависимостей lg N(ε) от lg(ε) для различных последовательных значений размерности и выбрать в качестве искомой ту размерность, начиная с которой график испытывает НАСЫЩЕНИЕ, т.е. угол наклона его линейной части перестает существенно изменяться. В случае временного ряда, представляющего собой вторую компоненту решения системы Рёсслера, видно, что можно принять в качестве размерности значение 3.
После определения размерности DEREK позволяет задать в максимально общем виде выражение для функции f(y1..yn,c1..cm). В качестве аппроксимирующего выражения для f(y1..yn,c1..cm) можно использовать полиномы или обобщенные полиномы, линейно зависящие от параметров c1..cm. Кроме того, соответствующая функция может отыскиваться в виде рационального выражения, числитель и знаменатель которого линейно зависят от параметров.
Для временного ряда, полученного при решении системы Рёсслера, выберем аппроксимирующее выражение в виде полинома второго порядка от переменных y1..yn:
Теперь DEREK позволяет подобрать оптимальные значения параметров и сохранить описание реконструированной системы обычным образом. После этого можно графически проанализировать степень близости решения y1(x) к исходному временному ряду.

Реконструкция произвольной динамической системы
Для того, чтобы не сложилось впечатление, что DEREK справляется только с хорошо известными модельными системами, мы предоставим пример реконструкции произвольной динамической системы, найденной в Сети (конечно же, совершенно случайно☻). В статье «Моделирование динамической системы по данным выходного сигнала» Т.С.Краснопольской и Е.Д.Печука рассматривается динамическая система плоского физического маятника с ограниченным возбуждением, которая описывается следующей системой уравнений:

Вот результат реконструкции ТРЕТЬЕЙ компоненты y3 решения системы (в качестве аппроксимирующих выражений для правой части выбраны полиномы третьего порядка):

Таким образом, DEREK может довольно успешно реконструировать абсолютно различные системы, не требуя от пользователя никаких специальных знаний. Никакого программирования, минимальное количество управляющих параметров, реконструкция в наиболее общем виде и очень наглядна! Разумеется, у DEREKа есть и некоторые недостатки, это прежде всего ограниченное количество точек временного ряда, доступное для обработки (не более 4000) и небольшое количество параметров (констант), подлежащих оптимизации при реконструкции (не более 30) .
Еще несколько примеров реконструкции находятся на странице «Еще о реконструкции».
Статьи с информацией о реконструкции динамических систем
-
Abarbanel H.D.I, Brown R., Sidorowich J., Tsimring L.S. «The analysis of observed chaotic data in physical systems»
-
Baake E., Baake M., Bock H.G., Briggs K.M. «Fitting ordinary differential equations to chaotic data»
-
Baker G.L., Gollub J.P., Blackburn J.A. «Inverting chaos: Extracting system parameters from experimental data»
-
Gorodetskyi V., Osadchuk M. «Analytic reconstruction of some dynamical systems»
-
Gousbet G., Letellier C. «Global vector-field reconstruction using a multivariate polynomial L2 approximation on nets»
на русском
Вот еще один пример временного ряда для реконструкции, его можно даже послушать!

